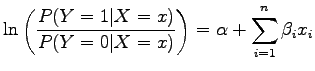4 Logistic Regression

One of the most wide-spread and effective classifiers in statistical learning, logistic regression, can be easily implemented in Alchemy Lite. Here, we only deal with binary predictors and dependent variables, but the extension to these is intuitive as well.

Logistic regression is a regression model of the form:

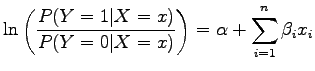$$\ln \left( \frac{P(Y = 1 \vert X = x)}{P(Y = 0 \vert X = x)} \right) = \alpha + \sum_{i = 1}^{n}{\beta_i x_i}$$ (1)

where $X$ is a vector of binary predictors and $Y$ is the dependent variable. So how do we describe this model in Markov logic? If we look at the model of Markov networks:

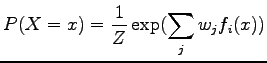$$P(X = x) = \frac{1}{Z}\exp(\sum_{j}{w_j f_i(x)})$$ (2)

this implies we need one feature for $Y$ and one feature for each $X_i$ ,$Y$ in order to arrive at the model

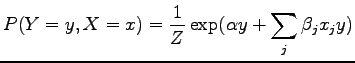$$P(Y = y,X = x) = \frac{1}{Z}\exp(\alpha y + \sum_{j}{\beta_j x_j y})$$ (3)

resulting in

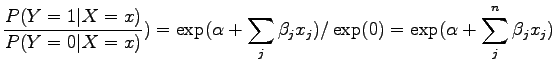$$\frac{P(Y = 1 \vert X = x)}{P(Y = 0 \vert X = x)}) = \exp(\alpha + \sum_{j}{\beta_j x_j}) / \exp(0) = \exp(\alpha + \sum_{j}^{n}{\beta_j x_j})$$ (4)

To represent this as an MLN, each parameter is represented as a weight corresponding to each formula, i.e. $\alpha \thickspace Y$ and for each $i$ , $\beta_i \thickspace X_i \wedge Y$

We demonstrate this on an example from the UCI machine learning data repository, the voting-records dataset, which contains yes/no votes of Congressmen on 16 issues. The class to be determined is ``Republican'' or ``Democrat'' (our $Y$ ), and each vote is a binary predictor (our $X_i$ ). Since weight learning is currently unavailable in Alchemy Lite, we trained a generative model using Alchemy (alchemy.cs.washington.edu) using the MLN:

Democrat(x)
!Democrat(x)
HandicappedInfants(x) ^ Democrat(x)
HandicappedInfants(x) ^ !Democrat(x)
WaterProjectCostSharing(x) ^ Democrat(x)
WaterProjectCostSharing(x) ^ !Democrat(x)
AdoptionOfTheBudgetResolution(x) ^ Democrat(x)
AdoptionOfTheBudgetResolution(x) ^ !Democrat(x)
...

where !Democrat(x) iff the person is a Republican.

So, the resulting .tml file (assuming there are 42 people in the world, from the number of people in the test data):

class WorldClass {
subparts Person[42];
}

class Person {
subclasses Democrat 4.88693, Republican -4.88693;
relations HandicappedInfants() -0.340171, 
          WaterProjectCostSharing() -0.18091, 
          AdoptionOfTheBudgetResolution() 0.102774,...; 
}

class Democrat {
relations HandicappedInfants() 0.558471, 
          WaterProjectCostSharing() -0.170664, 
          AdoptionOfTheBudgetResolution() 1.72017,...;
}

class Republican {
relations HandicappedInfants() -0.898642, 
          WaterProjectCostSharing() -0.0102457, 
          AdoptionOfTheBudgetResolution() -1.6174,...; 
}

We transformed the Alchemy .db file for the test data to one for Alchemy Lite:

WorldClass World {
Obj191 Person[1], Obj192 Person[2], Obj193 Person[3], ...
;
}

Person Obj191 {
!HandicappedInfants(), !WaterProjectCostSharing(), !AdoptionOfTheBudgetResolution(),... 
}

Person Obj192 {
!HandicappedInfants(), !WaterProjectCostSharing(), !AdoptionOfTheBudgetResolution(),... 
}

...

We can run MAP inference with

al -i voting.tml -o voting.result -e voting.db -map

which will print out the most likely subclasses of objects and truth values of all unknown relations. We can also query each person's political leaning separately. For example,

al -i voting.tml -o voting.result -e voting.db -q Is(World.Person[1],Democrat)